Using Integral Form of the Continuity Equation to Find Acceleration

The Continuity Equation: What Goes In Must Come Out

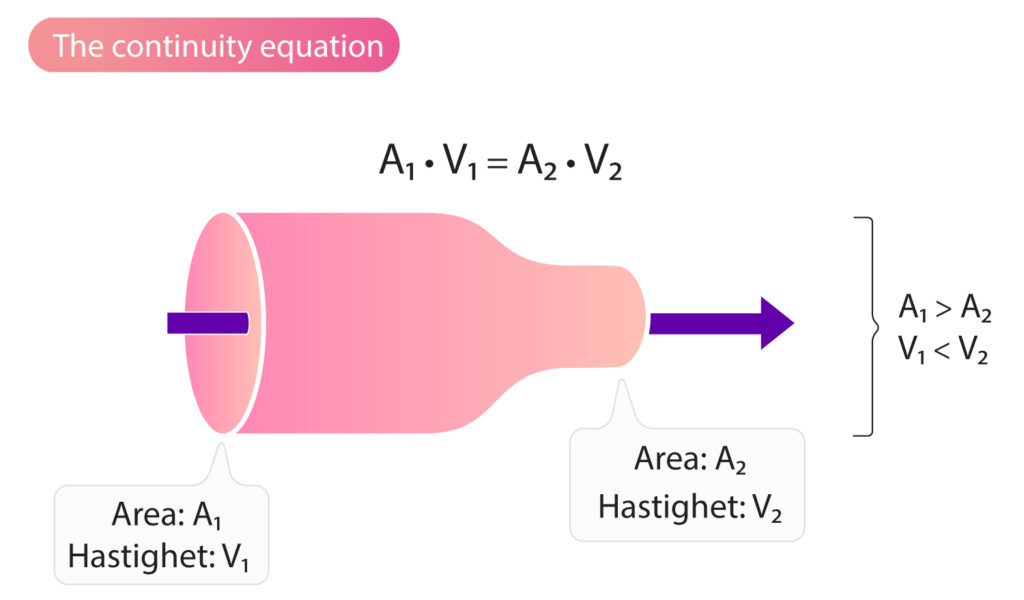
As previously discussed, stroke volume is usually calculated by measuring area and VTI (velocity time integral) in the LVOT (left ventricular outflow tract). However, stroke volume can also be calculated by quantifying the blood volume flowing over the mitral valve or the tricuspid valve. This is explained by the principle of continuity (the continuity equation), which states that the volume of blood flowing into a chamber must be equal to the volume flowing out of the same chamber (Figure 1). Thus, the blood volume flowing through the mitral valve in diastole is equal to the volume flowing through the aortic valve during systole (Figure 2). The continuity equation is explained by the fact that the velocity of blood is inversely related to the area of the orifice; velocity increases with diminishing area of the orifice, and vice versa.

Figure 1. The principle of continuity (the continuity equation).

Figure 2. The principle of continuity (the continuity equation) states that the volume of blood passing the mitral valve must be equal to the volume passing the aortic valve.

Stroke volume, the amount of blood ejected into the aorta, is calculated by measuring the area and VTI in the LVOT:

SV = area_LVOT • VTI_LVOT
SV = stroke volume; LVOT = left ventricular outflow tract; VTI = velocity time integral.

According to the formula, stroke volume is the product of area and VTI in LVOT. However, the continuity equation states that the stroke volume can be calculated by quantifying the volume flowing through the mitral valve, tricuspid valve or pulmonary valve. These volumes can be calculated using the same principle as for the aorta (i.e the product of the area and VTI). Although the continuity equation is correct, stroke volume is measured in the LVOT in the vast majority of cases, which is explained by the following:

• The aortic valve is easy to visualize and image quality is typically high in multiple views.
• The diameter of the aortic valve is relatively constant during systole; this is important because a representative diameter is crucial for calculation of the area.
• There is usually no – or only a negligible – amount of regurgitation in the aortic valve. The prevalence of tricuspid valve regurgitation and pulmonic valve regurgitation is relatively high.

To calculate the flow (volume) over the mitral valve, the maximum diameter of the valve is measured in diastole in apical four-chamber view. VTI is obtained in the same view with the sample volume placed in the center of the mitral annulus.

SV_mitral = area_mitral • VTI_mitral

To calculate the flow over the tricuspid valve, the diameter and VTI are measured in the RVOT (Right Ventricular Outflow Tract). The measurements are made at the aortic valve plane in the parasternal short-axis view.

SV_tricuspid = Area_RVOT • VTI_RVOT

Continuity equation and valvular regurgitation

The continuity equation implies that the amount of blood flowing into the left ventricle (across the mitral valve) is equal to the amount of blood flowing out of the left ventricle (across the aortic valve). In other words, the stroke volume across the aortic valve is equivalent to the stroke volume across the mitral valve. This principle can be used to quantify regurgitations and stenoses. For example, in mitral regurgitation, the regurgitant volume can be quantified by calculating the difference in stroke volume across the aortic valve and the mitral valve, according to the formula:

RV_mitral = SV_mitral – SV_aorta
RV = regurgitant volume; mitral = mitral valve.

Similarly, the volume leaking back into the left ventricle in aortic regurgitation can be calculated using the following formula:

RV_aorta = SV_aorta – SV_mitralis

Grading of the severity of stenoses using the continuity equation

All valvular stenoses must be graded in order to optimize management according to disease severity. The most important parameter, for grading of stenoses, is the opening area of the stenosis. The smaller the area, the more pronounced the stenosis and, accordingly, the greater the hemodynamic effect. The continuity equation can be used to calculate the area of the valve. The following formula indicates that flow over the mitral valve is equivalent to flow over the aortic valve:

area_mitralis • VTI_mitralis= area_aorta • VTI_aorta

The formula shows that either valve area can be calculated by measuring the other three variables.

hooksafterely39.blogspot.com

Source: https://ecgwaves.com/topic/the-continuity-equation/

Share this post